CSC204 - Lab 1
Cartographic Projections

Assigned Jan 22nd
Due Jan 25th 2pm

UPDATE

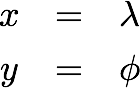
We commonly think of latitude and longitude in degrees, however the projections in this lab are expecting them to be in radians, which is scaled so that 360 degrees is equal to 2 * pi radians. The Math class in Java has a helpful function toRadians(double angdeg), which will convert the variable angdeg in degrees into radians. You will need to do this to both of the parameters entered on the command line.

Overview

In this lab, you will gain practice performing mathematical calculations in Java and following the handin process for labs and homeworks.

Description

In today's society, traveling from one location to another is made easier through the use of GPS systems and route-planning programs such as Google Maps. However, our world is spherical and 3D, but our maps and representations are in 2D and flat. The question of the "best" way to translate from one to the other is studied in Cartography. Since ancient times, cartographers have tried to balance the accuracy of land-mass size, distance, and bearing when creating projections onto a flat surface.

In this lab you will explore three such projections and compare their resulting distance deformations. You must write a Java program that can be executed in the following manner:

java Projection <Latitude> <Longitude>

which takes two floating-point doubles as input from the command line.

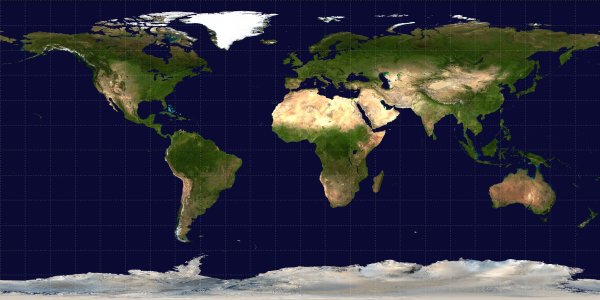Step 1 - Equirectangular

The Equirectangular projection is a direct translation of latitude and longitude into x, y coordinates. This is historically the oldest projection, with its biggest strength being that it is very easy to calculate.

Given a Latitude phi and Longitude lambda and using the Prime Meridian as the center of the map, we can find the x, y ordered pair projection by:

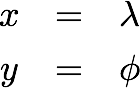
Calculate these x and y coordinates in Java, and display the output to the screen in the following format

EQUI: x = ???, y = ???

where the ??? are replaced by the calculated coordinates.

Step 2 - Mercator

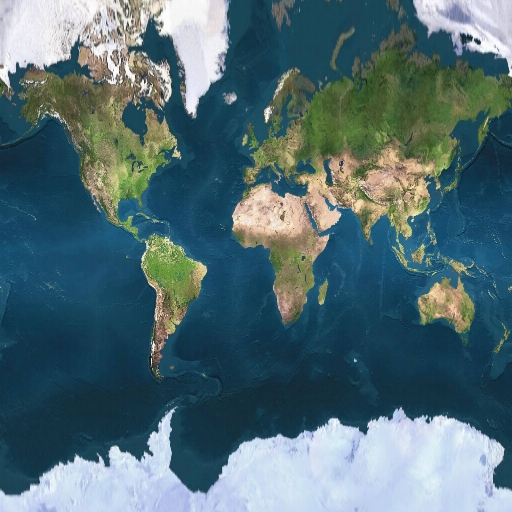The Mercator Projection, formulated in 1569 by Gerardus Mercator, is the most commonly used projection and is seen on elementary school walls across America. It has the property that compass bearings are accurately displayed, and is extremely useful for nautical purposes.

Given a Latitude phi and Longitude lambda and using the Prime Meridian as the center of the map, we can find the x, y ordered pair projection by:

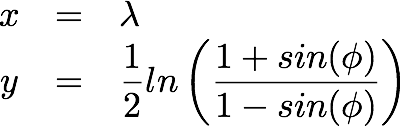
Calculate these x and y coordinates in Java, and display the output to the screen in the following format

MERC: x = ???, y = ???

where the ??? are replaced by the calculated coordinates.

Step 3 - Winkel Tripel

The Winkel Tripel projection was adopted by the National Geographic Society in 1998 as their official project. It is an average of two other projections, and provides a low amount of individual distortion across the whole map.

Given a Latitude phi and Longitude lambda and using the Prime Meridian as the center of the map, we can find the x, y ordered pair projection by:

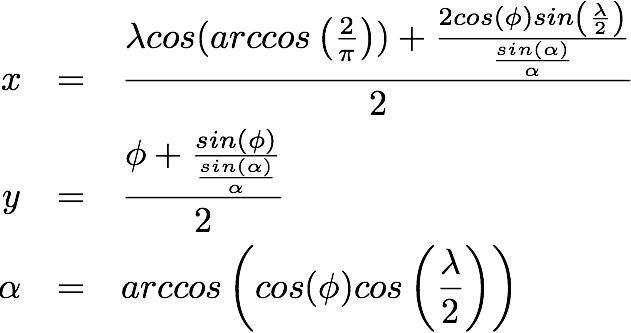
Calculate these x and y coordinates in Java, and display the output to the screen in the following format

WT: x = ???, y = ???

where the ??? are replaced by the calculated coordinates.

Step 4 - Distance of Deformation

Each projection will place our given latitude and longitude in a slightly different x, y coordinate point. As we are not yet using graphics in our programs, we are only able to distinguish these projections based on the distance between the projected x, y points, using the following formula for Euclidean distance.

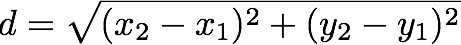
Calculate the distance between your given latitude and longitude points for each pairing of the three discussed projections. Display this output to the screen in the following format

EQUI vs MERC: ???

EQUI vs WT: ???

MERC vs WT: ???

where the ??? are replaced by the calculated distances.

Evaluation

Write a short evaluation of your experience with this lab. You must answer the following questions:
  1. What is the output of your program using the coordinates for the Nashville at 36.12 degrees Latitude and -86.67 degrees Longitude?
  2. What is the output of your program using the coordinates for Shreveport at 32.47 degrees Latitude and -93.77 degrees Longitude?
  3. We represented latitude and longitude as doubles. What changes would we need to make in order to use degrees, minutes and seconds?
  4. Which projection method would you choose and why?

What to Hand In

To hand in your Lab 1 files, follow the steps listed below from the Wright Lab computers:
  1. Open the Terminal application.
  2. SSH with ssh username@cs.centenary.edu to connect with the cs server.
  3. Type in your password.
  4. Make a new directory with mkdir csc204/lab1
  5. Change the permissions with chmod 700 csc204/lab1
  6. Set permissions for grading with setfacl -m u:mgoadric:rx csc204/lab1
  7. Log out of the cs server with logout
  8. Change to the directory where you have your files on the local computer. (In class, we have been using cd csc204
  9. Securely copy your java file to your directory with scp Projection.java username@cs.centenary.edu:"csc204/lab1"
  10. Securely copy your evaluation file to your directory with scp lab1_evaluation.txt username@cs.centenary.edu:"csc204/lab1"
© Mark Goadrich 2007, Centenary College of Louisiana