CSC207 - Lab 9
Cryptogram Decipherment

Assigned October 27th 2 p.m.
Due October 29th 4 p.m.

Overview

Continuing on the topic of decipherment, we now look at more complicated substitution ciphers. We will build a program to assist us in deciphering cryptograms using Python dictionaries.

Materials

Description

Last lab, we explored finding automatic solutions to the Caesar Cipher, where the alphabet was rotated to provide a rudimentary form of encryption. We demonstrated that messages encoded in a Caesar Cipher are easily decoded. A stronger encryption method is the Substitution Cipher. Examples of substitution ciphers can be found in the Sherlock Holmes short story called The Dancing Men, and in the Alien languages from the cartoon Futurama.

In a substitution cipher, a letter can be replaced by any other letter or symbol, such that each letter is only used once per original letter. For example, given the mapping for Alien Language 1 below:

Alien Language 1

We can decode the sign behind Bender here to say

TASTY HUMAN BURGERS

If we know the mapping for substitution, decipherment is easy, however, we are often given encrypted text, and we must discover the map on our own. In this lab, we will be building a program to assist the user in decoding Cryptograms, a common version of a substitution cipher found in the daily newspapers. The program will use Python dictionaries to map one character to another for translation, and provide the current best mapping based on character frequencies.

Data

Quote 1:

GPYTKM! YLNDQ GPBQVF KBOBQV BQ D LQMPCVCTLQM JDOP, RYBJY YDF D NTLIY TWPQ ITRDCMF IYP KBVYI DQM CPDJYBQV DKK DKTQV IYP JDOP; YPCP IYPX YDOP GPPQ SCTN IYPBC JYBKMYTTM, DQM YDOP IYPBC KPVF DQM QPJHF JYDBQPM FT IYDI IYPX JDQQTI NTOP, DQM JDQ TQKX FPP GPSTCP IYPN, GPBQV WCPOPQIPM GX IYP JYDBQF SCTN ILCQBQV CTLQM IYPBC YPDMF. DGTOP DQM GPYBQM IYPN D SBCP BF GKDABQV DI D MBFIDQJP, DQM GPIRPPQ IYP SBCP DQM IYP WCBFTQPCF IYPCP BF D CDBFPM RDX; DQM XTL RBKK FPP, BS XTL KTTH, D KTR RDKK GLBKI DKTQV IYP RDX, KBHP IYP FJCPPQ RYBJY NDCBTQPIIP WKDXPCF YDOP BQ SCTQI TS IYPN, TOPC RYBJY IYPX FYTR IYP WLWWPIF.

Quote 2:

JUVR GBJU W ZAHR ZSJ VXAYENRU WYAVR WUE PJP DJGUE W VWCR. WYAVR QWAE: "QBYRUEAE! A SAYY RWZ ZXR VWCR." PJP QWAE: "UJ, ZXWZ AQ UJZ DWAN! SR DJGUE ZXR VWCR ZJFRZXRN, WUE SR QXJGYE QXWNR WUE QXWNR WYACR; XWYD DJN OJG WUE XWYD DJN HR." WU WNFGHRUZ RUQGRE PRZSRRU ZXRH. WYJUF VWHR WU WEGYZ SXJ QWAE: "OJG QXJGYEUZ DAFXZ WPJGZ ZXAQ; OJG QXJGYE VJHBNJHAQR, WUE FATR WYAVR ZXNRR-KGWNZRNQ JD ZXR VWCR." BWNWBXNWQRE DNJH NWOHJUE QHGYYOWU

Step 1

As with a Caesar cipher, information will be leaked from the ciphertext in the form of the frequency counts of each letter. Recall the standard frequency counts for words in the English language:

Figure 1: English letter frequencies

However, we no longer have only 25 possibilities for decryption, since we are substituting letters individually instead of rotating them as a whole. In fact, there are 1.551121 x 10 ^ 25 (25!) possible ways to decrypt the text, since A can stand for any of the 25 other letters, B then stands for one of the 24 left, etc.

Our approach here will be what is called a greedy search. We will select the letter-match that looks the most probable, then the second most probable, until we have chosen 26 matchings, one for each letter in the alphabet. We will choose the most probable match by saying the highest-frequency letter in the ciphertext will be mapped to the highest-frequency letter in the reference text, and then remove these letters from being selected in subsequent matchings. This will not be a great solution, but will give us somewhere to start.

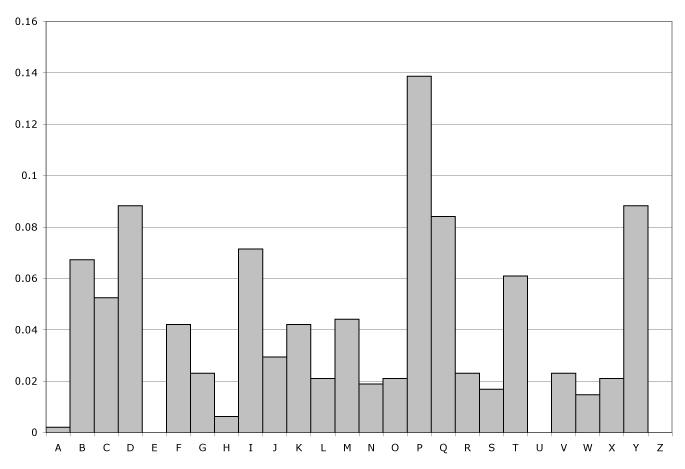
Figure 2: Ciphertext letter frequencies

For example, if we were using the greedy search on the above frequencies from Figure 2 from a ciphertext and the earlier reference frequencies of Figure 1, we would first pick P stand for E since they are both the highest peaks. The next two highest peaks are Y and T, then D and A, etc, matching them one by one until all 26 letters are matched.

Create a function frequency_map(o_freq, e_freq) that will return a dictionary mapping of characters based on the above greedy search.

Test your function in the interpreter. Use Chapter One of Alice's Adventures in Wonderland as your reference text to calculate expected frequencies in e_freq, and Quote 1 from the Evaluation section below as your ciphertext to calculate o_freq. Your returned frequency map should be 

{'A': 'J', 'C': 'S', 'B': 'I', 'E': 'Q', 'D': 'T', 'G': 'U', 'F': 'L', 'I': 'H', 
 'H': 'V', 'K': 'D', 'J': 'W', 'M': 'R', 'L': 'C', 'O': 'Y', 'N': 'B', 'Q': 'A', 
 'P': 'E', 'S': 'P', 'R': 'G', 'U': 'X', 'T': 'N', 'W': 'K', 'V': 'F', 'Y': 'O', 
 'X': 'M', 'Z': 'Z'}

Step 2

The next function we create will use the map from frequency_map and translate our ciphertext into plaintext. For each character in our text that is a letter in "ABCDEFGHIJKLMNOPQRSTUVWXYZ", look up that letter as a key in the map and substitute the associated value into the text. Write a function decrypt_sub(s, map) to decrypt the string s with the substitution map.

Test your code on Quote 1 and the frequency map you calculated in Step 1. It should return the following text:

UEONDR! OCBTA UEIAFL DIYIAF IA T CARESFSNCAR WTYE, GOIWO OTL T BNCHO NKEA HNGTSRL HOE DIFOH TAR SETWOIAF TDD TDNAF HOE WTYE; OESE HOEM OTYE UEEA PSNB HOEIS WOIDRONNR, TAR OTYE HOEIS DEFL TAR AEWVL WOTIAER LN HOTH HOEM WTAANH BNYE, TAR WTA NADM LEE UEPNSE HOEB, UEIAF KSEYEAHER UM HOE WOTIAL PSNB HCSAIAF SNCAR HOEIS OETRL. TUNYE TAR UEOIAR HOEB T PISE IL UDTJIAF TH T RILHTAWE, TAR UEHGEEA HOE PISE TAR HOE KSILNAESL HOESE IL T STILER GTM; TAR MNC GIDD LEE, IP MNC DNNV, T DNG GTDD UCIDH TDNAF HOE GTM, DIVE HOE LWSEEA GOIWO BTSINAEHHE KDTMESL OTYE IA PSNAH NP HOEB, NYES GOIWO HOEM LONG HOE KCKKEHL.

Step 3

This may be the mapping that is likely according to frequency counts, but as we see above, this is not perfect, the message is still unintelligible. Almost always, this will not be the right translation. To find the correct message, we must revise our map by interacting with the user.

Write a function called user_map(map) which brings in a current map from the user and prompts them to add one more character key and value to this map. This augmented map is then returned.

One restriction we will place on the user is that they are not allowed to map two different letters to the same letter. In other words, a letter cannot appear twice in the list of values inside our character map. If the user tries to do this, you should tell them that is an invalid mapping, and prompt them again for a new mapping.

Test out your function by starting with the empty map {} and adding a new character key-value map of G -> B. Then use this map as your input and add a new mapping of Y -> H.

Step 4

With this new incremental map from the user, we need to use that and revise our previous map-creation function. Revise frequency_map(o_freq, e_freq) from Step 1 into frequency_map(map, o_freq, e_freq)to take into account the user map. It should remove from consideration any characters mappings the user has specified, and fill in the rest based on the remaining frequency counts, to return a full map.

Test your code with your frequencies from Step 1 and the map from Step 3. Your function should generate the following frequency map: 

{'A': 'J', 'C': 'S', 'B': 'I', 'E': 'Q', 'D': 'T', 'F': 'L', 'I': 'A', 'H': 'V', 
 'K': 'D', 'J': 'W', 'M': 'R', 'L': 'F', 'O': 'C', 'N': 'M', 'Q': 'O', 'P': 'E', 
 'S': 'P', 'R': 'U', 'U': 'X', 'T': 'N', 'W': 'K', 'V': 'G', 'X': 'Y', 'Z': 'Z',
 'G': 'B', 'Y': 'H'}

Step 5

Now that we have all our basic functions built and tested, we can create the final main function to power this Cryptogram Assistant. Your main function should at least do: You may find more pieces of information useful as the user; add these as you feel appropriate in a format that you can understand.

Evaluation

Use your interactive program to solve the two cryptoquotes in the Data section. You might find some tips on solving Cryptoquotes helpful. Write up your found answers and the character map in a file called lab9_evaluation.txt

What to Hand In

Log in to cs.centenary.edu through either Secure FTP or WinSCP using your cs login and password. Create a subdirectory from csc207 called lab9. Copy your substitution.py project into this directory. Make sure you have followed the Python Style Guide, and have run your project through the Automated Style Checker.

You must hand in:

© Mark Goadrich 2007, Centenary College of Louisiana