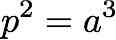
One astronomer who made a major advance in the understanding of our solar system and
astrophysics in general was
Johannes Kepler.
In fact, NASA plans to launch a satellite to search for habitable planets in 2009, and has
named this mission after Kepler.
In the early 1600s he published his now-famous three laws of planetary motion.
These laws, based on years of stellar and planetary observation by
Tycho Brahe,
finally fixed any lingering anomalies in the
Copernican theory
that the Earth and other planets
revolved around the Sun. The first law states that the planets orbited the Sun in ellipses with
the Sun at one foci. The second law states that planets would travel faster the closer they are
to the sun and slower when farther away.
The third law describes the relationship Kepler observed between a planet's distance from the sun and the time it takes to make one complete orbit around the sun. Kepler stated that the square of a planet's orbital period in years was equal to that planet's distance from the sun in Astronomical Units (AU) cubed, where and AU is the average distance of the Earth to the Sun (149 million kilometers).
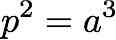
orbit_kepler.py for Kepler's Third Law
of planetary motion.
This program will ask the user for the name of the planet
and its average distance from the sun in astronomical units (AU).
It should then calculate the orbital period
of this planet in years and display the result to the user. Make sure to follow
the Python Style Guide when writing your program.
Test your code with the following values for planets orbiting the Sun:
| Planet | AU from Sun | Period |
|---|---|---|
| Earth | 1 | 1 |
| Saturn | 9.58201720 | 29.660974748248961 |
| Mercury | 0.38709821 | 0.24084173359179098 |
In 1687, Isaac Newton followed
up on the laws of Kepler to publish his
Principia Mathematica. In this work, he explained that it was the
universal force of gravity which tied together the motion of the planets and the motion
of objects here on Earth. Kepler's third law was found to be a special case of a more general
law about the gravitational attraction between two objects in space, M1 and M2. Now, instead
of Kepler's law being tied to the Earth and the Sun, we can now calculate the orbital
period of any planet around any star as long as we know both their masses and the
average distance of the star from the planet.
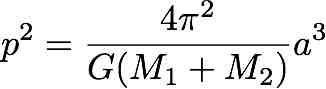
The big G in Newton's equation is the Gravitational Constant from physics, and is in terms of meters cubed over kilograms times seconds squared.
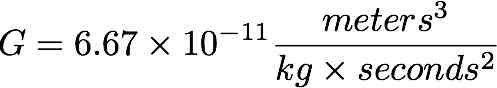
orbit_kepler.py into orbit_newton.py
to use Newton's reformulation of Kepler's Third Law. The user will be asked to enter the
name of the planet, the average distance from the star in AUs, the mass of the star in kilograms,
and the mass of the planet in kilograms. Since Newton's law uses meters instead of
AU, you will have to convert the user's input into the appropriate value, using the
definition of 1 AU as 149 million kilometers. Calculate the orbital period of the planet next,
and output the result to the user. Your formula will calculate the period in seconds, but
you should convert your answer and return to the user the number of days in the orbital period.
Evaluate orbit_newton.py using the following data about the red dwarf star
Gliese 581 and the three planets
detected so far which orbit this star. Current scientific research is
focused on this star system since
planet c is close in size to Earth and is
a comparable distance from Gliese 581 (reported in April 2007), meaning it may lie in the
Habitable Zone for life. Report your
results for the orbital period of these planets in the lab3_evaluation.txt
described below.
| Planet | AU from Star | Mass in kg |
|---|---|---|
| b | 0.041 | 9.30314 X 10^24 |
| c | 0.073 | 3.03776 X 10^24 |
| d | 0.25 | 4.55664 X 10^24 |
math.pi,
namely 3.1415926535897931. This is only an estimate of Pi; others have calculated
1,000,000 digits of Pi, but this is still only an estimate of this irrational number.
Test out the sensitivity of your calculations above to different values of Pi, using 3.14 and
3.14159, and record your results in lab3_evaluation.txt. Be sure to return your
code to use the original math.pi before you turn in your code.
lab3_evaluation.txt:
orbit_kepler.py
when writing orbit_newton.py?
orbit_newton.py, the Mass of the planet or the distance from the star? Why?
orbit_newton.py?
cs.centenary.edu.
Now within your csc207 directory, create a new directory called lab3.
Copy the above three files into this directory.
Make sure you run orbit_kepler.py and orbit_newton.py
through the Python
style guide checking program before you turn in your work. If you worked with a
partner, you both must hand in the files you wrote, with both of your names in the header
at the top of the file.