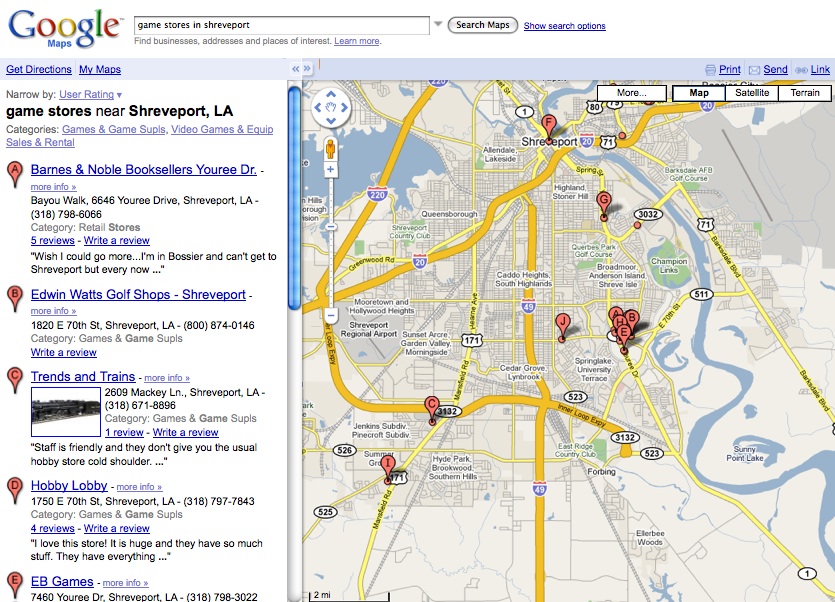

We would like to efficiently search this space for nearby locations. The naive way to do this would be to walk through a list of objects and sort them based on their distance from the starting location, but with 1,000,000 entries, this is prohibitive.
In this project, you will implement a version of proximity search using a QuadTree and a Heap. A QuadTree is a two-dimensional version of a Binary Tree, such that instead of a left and a right, there is a NW, NE, SW and SE child. The particular version we will implement is called a PR (Point Region) QuadTree. Each child is exactly 1/4 of the size of it's parent.
To implement our QuadTree and proximity search, we will need a number of smaller instantiable objects. Each object should have the usual accessor and mutator methods for each data member, and a toString and equals method. Feel free to add other objects and methods you see fit to complete this project.
Data Members
double x : for the x coordinate
double y : for the y coordinate
double distance(Point p) : returns the Euclidean distance between two points
boolean equals(Object o) : returns true when the two points have the same x and y coordinates.
Data Members
double dist : for saving the distance to the most recent location.
void setDistance(double d) : saves the most recent distance
double getDistance() : returns the saved distance
int compareTo(ProxDist pd) : returns a negative integer if this is less than pd,
a positive integer if this is greater than pd, otherwise returns 0 if they are equal.
Data Members
Point p : for the x,y coordinate
String name : for the name of the location
double distance(ProxDist pd) : calculates the distance between this Location
and a QuadNode object. If the ProxDist object a Location, return the distance bewteen
the two Points of the Locations. Otherwise, return the minimum distance between the Location's
Point and the four sides of the QuadNode.
Data Members
QuadNode[] children : to store the NW, NE, SW, and SE children of the tree
Location item : for the data, if this is a leaf
Point upperLeft : for the upper left Point of the rectangle
Point lowerRight : for the lower right Point of the rectangle
boolean isLeaf() : returns true if all of the children are null
Data Members
QuadNode root : for the top-most element of the tree
Point upperLeft : for the minimum bounds of the tree
Point lowerRight : for the maximum bounds of the tree
void add(Location item) : adds a Location item to this QuadTree. If the
root is null, create the root QuadNode with the initial upperLeft and lowerRight bounds.
If the root is not null, determine which subquadrant holds this Location. If that child exists, then repeat, trying to add the Location to this child, otherwise create a new leaf containing the Location. If the new Location is the same as the existing Location at this QuadNode, then discard the new Location.
If the QuadNode where the new leaf was added was a leaf (contains a Location itself and had no children), then set the current item to null and recursivelly call the add method to place the current item.
Location remove(Location item) : removes the closest Location in this QuadTree
to item. Use the proximitySearch below to find the closest item, then search for it in the tree. Remove the leaf QuadNode pointing to this item from the parent. If this results in a QuadNode with only one child, then remove this last child and set its Location to the Location of its only child, and repeat for this node's parent.
ArrayList<Location> proximitySearch(Location item, int k) : returns
the k closest elements to the Location item.
Create a Heap<ProxDist> to keep the distances found in a priority queue. Initialize this Heap with the object based on the QuadTree root. Then, while the Heap still has elements or the ArrayList of Locations found is less than k, remove the first item from the Heap. If it represents an individual Location, then add it to the ArrayList of Locations to return. Otherwise, if it is a leaf, find the distance to its Location and add this Location to the Heap. If it is a QuadNode with children, then for each calculate the distance of the query Location to each child QuadNode, and add them to the Heap.
main is the main method, and responsible for running your program.
The main method should begin by asking the user for a file to load with the geographical data. The first line of this file will contain four numbers. The first two are the minimum x,y coordinates for the upper left corner, and the second two are the maximum x,y coordinates for the lower right corner. All subsequent lines will be three data values, the first being the x coordinate, the second being the y coordinate, and the third being the name of the location. Your program should add the rest of this data into a QuadTree following the QuadTree construction algorithm above.
The user is repeatedly asked if they want to QUERY, ADD, REMOVE, or QUIT the program.
If the user wants to QUERY, ask them for a starting location x and y, and the number of results they would like to see. The user's x and y must be within the bounds loaded from the file, and the number of results must be greater than 0.
Your program should then begin searching the QuadTree for locations near to the starting location. Internally, you should use a Heap (the code is linked below) to store your ProxDist objects, such that the closest QuadNode is searched next, and the children of that QuadNode are placed on the Heap to be found later.
The results of this search are then displayed to the user in the format of Name, Distance, X, Y, with one entry per line.
You can test your code with the following data files:
If the user wants to ADD, ask them for an x and y coordinate and the name of the new location, then add this to the QuadTree.
If the user wants to REMOVE, ask them for an x and y coordinate, and then remove the closest Location from the QuadTree to that location, printing off the name of this location when it is removed.
If the user wants to QUIT, exit the program gracefully.
project6.