CSCI 150 - Lab 12
Fractal Recursion
Overview
Certain elements of mathematics can be naturally described by recursion, as we saw with the
factorial function. Today, we will look
into the mathematics of fractals and how some of their properties can be described with recursion.
Materials
Description
We will be using the Turtle module in python for our fractals today, like
Sierpinski's Triangle,
Koch Snowflake, and the
Dragon Curve.
To access the Turtle module
and define a turtle, we use the following lines of code:
import turtle
t = turtle.Turtle()
With our turtle t, we can make this turtle navigate around the screen, similar to our
programming with Scratch.
Some commands for the turtle are:
- movement around the screen:
t.forward(n), t.back(n) will move the
turtle n pixels in the current direction, t.goto(x, y) will go to a
particular location on the screen.
- changing direction:
t.right(d), t.left(d) will turn the turtle left or right
by d degrees.
- draw a dot on the screen of a certain size:
t.dot(size)
- put the pen down or pick the pen up:
t.penup(), t.pendown()
Step 1
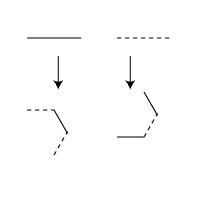
The first type of fractal we will examine uses a simple rewrite rule. Iterative, we can
replace a straight line with four new smaller lines, connected up with the following angles.
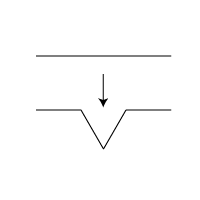
Now we can repeat, at each level, replace these four new lines in the same manner. Write a recursive
function in a file called fractal.pyto have the turtle draw this replacement, with the base case being to draw a line, and
the recursive case be to draw these four lines at 1/3 the original distance.
Step 2
Create functions for the following transformations:
Koch 2
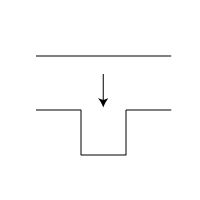
Koch 3
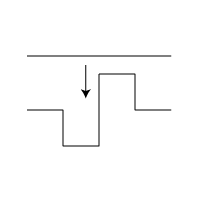
C-curve
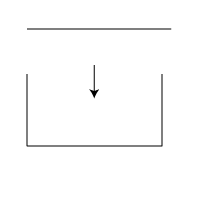
Step 3
These next two are a little different. They each require two functions for
replacement instead of just one above.
Dragon Curve
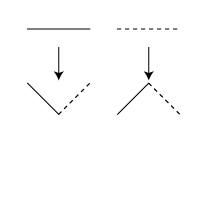
Sierpinski's Triangle
Step 4
Create your own replacement rule for your personal
fractal, and write code to draw this new fractal.
What to Hand In
Log in to Moodle and handin your code. Make sure
you have followed the Python Style Guide, and
have run your project through the Automated Style Checker.
You must hand in:
© Mark Goadrich, Hendrix






