Course Details
Textbook
 |
RECOMMENDED ONLY An Introduction to Formal Languages and Automata by Peter Linz, 2016 ISBN: 978-1284077247 Find this book at Amazon |
 |
JFLAP V7.0 |
Overview
Covers basic topics in automata, computability, and complexity theory, including: models of computation (finite automata, Turing machines and RAMs); regular sets and expressions; recursive, r.e., and non-r.e. sets and their basic closure properties; complexity classes; determinism vs. non-determinism, with and without resource bounds; reductions and completeness; practice with NP- and P-completeness proofs; and the complexity of optimization and approximation problems.By the end of this course, you should be able to:
- describe the relationship between formal languages and machines that can recognize them;
- describe the hierarchy of finite automaton, stack machines, and Turing machines;
- state the definitions of the primary concepts of the course, such as decidability, intractability, determinism, computability, recursive enumerability, and the Church-Turing thesis;
- understand the difference between decidable and undecidable problems;
- apply reducibility techniques to classify problems;
- classify a given decidable problem as belonging to P, NP, NP-complete, or exponential time complexity classes;
- work together to teach each other course material;
- present a clear, concise solution to a problem in written form;
- present a clear, concise solution to a problem or summary of a topic orally.
Prerequisites
MATH 240.Participation and Absences
You are expected to attend class and participate in discussions every day, answering questions, asking questions, presenting material, etc.You may miss three non-presentation days with no penalty. These can be for sports travel, school sanctioned activities, sick, etc. You are expected to make up any work you miss through these absences. Every subsequent absence will result in a 4% penalty on your final grade.
Disabilities
It is the policy of Hendrix College to accommodate students with disabilities, pursuant to federal and state law. Students should contact Julie Brown in the Office of Academic Success (505.2954; brownj@hendrix.edu) to begin the accommodation process. Any student seeking accommodation in relation to a recognized disability should inform the instructor at the beginning of the course.Academic Honor
As stated in the Hendrix Academic Integrity Policy, all students have agreed to adhere to the following principles:- All students have an equal right to their opinions and to receive constructive criticism.
- Students should positively engage the course material and encourage their classmates to do the same.
- No students should gain an unfair advantage or violate their peers' commitment to honest work and genuine effort. It follows that any work that a student submits for class will be that student's own work. The amount of cooperation undertaken with other students, the consistency and accuracy of work, and the test-taking procedure should adhere to those guidelines that the instructor provides.
- Members of the Hendrix community value and uphold academic integrity because we recognize that scholarly pursuits are aimed at increasing the shared body of knowledge and that the full disclosure of sources is the most effective way to ensure accountability to both ourselves and our colleagues.
Extensions
Extensions are only given when circumstances beyond your control (e.g. being sick, choir or sports travel) prevent you from completing a project on time. You must notify me either by email or phone of your circumstances well in advance of the due date.Syllabus
We will be covering most of the recommended textbook following the format in the table of contents. We will also be using additional supplemental material such as relevant web-pages and background material. Additional readings will be assigned before material will be covered in class. You are expected to review the material and come to class prepared.Homework
You will have many many homework problems in this course, with problems assigned almost every day, for a total of 45% of your final grade.There will be individual as well as group portions to most homeworks. Individual questions must be completed and submitted individually. You are required to complete all individual sections and your group section.
- HW1
Individual - Survey
Group - Problems
- HW2
Individual/Group - Problems
- HW3
Individual/Group - Problems
- HW4
Individual/Group - Problems
- HW5
Individual/Group - Problems
- HW6
Individual/Group - Problems
- HW7
Individual/Group - Problems
- HW8
Individual/Group - Problems
- HW9
Individual/Group - Problems
- HW10
Individual/Group - Problems
- HW11
Group - Problems
- HW12
Group - Problems
- HW13
Visit the Complexity Zoo
All homeworks must be written using LaTeX and turned in as a PDF on Moodle. There are many resources available for LaTeX on the web, including the LaTeX Math Symbols, Detexify, and a WikiBook on LaTeX.
I recommend using ShareLaTeX to create your documents, it is an online implementation of LaTeX that allows for collaboration.
Here is a great template LaTeX file for homework assignments.
Groups
You will be rotating through assigned groups for your homeworks over the course of the semester.For each question, one member of your group will be randomly chosen to present your group's work in class. This presenter must also be prepared to answer questions first from members of the other groups and then from the instructor.
The goal of these presentations is to work as a class and as a group to teach each other the concepts in theory of computation and to improve each other's presentation skills.
If the presenter is successful, all members of the group are awarded 3 points.
If there are major errors in the written answer, the accuracy of the answer, or the oral presentation skills, the question will be remanded to the group. Within one week, in future class sessions, this original presenter must ask to present their question again. If successful after the second presentation, the group will earn 2 points. If there are further concerns, the question will be once again remanded to the group, and can be presented one more final time within one week, where a successful presentation will earn the group 1 point.
If the presentation is successful, but there are minor errors in the written answer, the accuracy of the answer, or the oral presentation skills, 0.5 points will be deducted from this group score.
If any group member is absent from class without a valid excuse when a group is awarded points, this member will receive 0 points.
If an absent group member without a valid excuse is randomly chosen to present, another group member will be selected and 1 point will be deducted from this group score.
4 points per individual per day will also be awarded for asking insightful questions of presentations of other groups.
Your total points accumulated are divided by the total number of questions your groups have been asked to answer, and then your final percentage for this section is determined by the following formula (bounded below by 0 and above by 110).
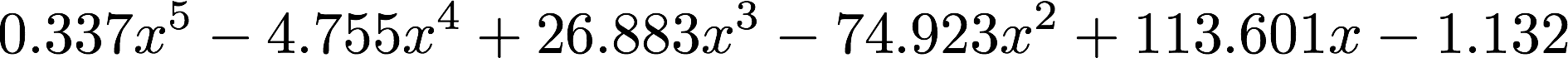
Therefore, to earn the maximum number of points, you are responsible for ensuring that all group members are prepared to accurately present all questions assigned to your group, and that you engage other groups through insightful questions and constructive feedback.
First Grouping
- Hall, Hong, Murray, Thomasson, Wycoff
- Barker, Bayer, Belding, Dietrich
- Ali, Hirrel, Mershon, Yalom
Second Grouping
- Ali, Dietrich, Mershon, Thomasson
- Barker, Belding, Hall, Murray
- Baer, Hirrel, Hong, Wycoff, Yalom
Third Grouping
- Barker, Hirrel, Mershon, Wycoff, Murray
- Baer, Hall, Thomasson, Yalom
- Ali, Belding, Dietrich, Hong
Exams
There will be three exams, respectively worth 10%, 20%, and 25% of your final grade. They will be take-home exams and will cover material from the homeworks.- Exam 1: Due September 20
- Exam 2: Due October 30
- Final: Due Final Exam period December 12 8:30am
Grading
Your final grade for this course will be based on the Homework, Exams and Presentations described above.
|
| ||||||||||||||||||||||||
© Mark Goadrich, Hendrix College