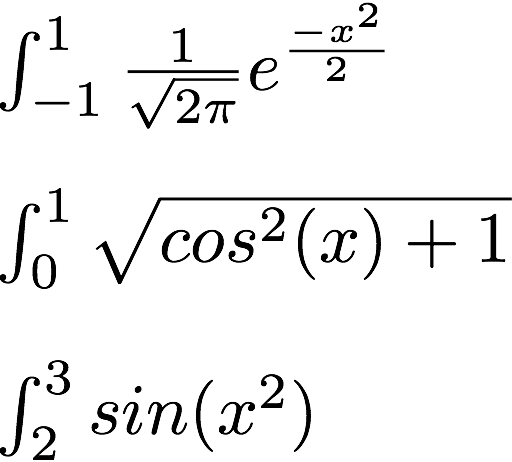
A casino offers a game of chance for a single player in which a fair coin is tossed at each stage. The pot starts at 2 dollars and is doubled every time a head appears. The first time a tail appears, the game ends and the player wins whatever is in the pot. Thus the player wins 2 dollars if a tail appears on the first toss, 4 dollars if a head appears on the first toss and a tail on the second, and so on. In short, the player wins 2k dollars, where k equals number of tosses.
If we assume the casino can pay out any winning amount, the expected value for this game is infinity. This is weird.
Explore different values for the maximum payout from the casino using a Monte Carlo simulation. Plot the maximum payout versus your calculated expected values, for payouts from 1 to 1,000,000.
What do you think would be a fair price to pay the casino for entering the game?
mc_integrate(func, a, b)to integrate
a given function over a specified interval from a to b using
Monte Carlo integration.
Demonstrate your method by estimating the integral for the following three functions.